Related:
a dynamic programming method used to find the best way to align sequences by comparing the two sequence on a dissimilarity or similarity matrix, and scoring them on match by assigning them a number inside the box of the matrix
visual work-through of the problem using similarity matrix based scoring1
Overall steps
- create the matrix
- import and align the two sequences at the top and side of the matrix
- traceback
- determine potential alignments
Idea behind scoring: matches, mismatches, and gaps all have different values. Based on the scores, N-W gives an “optimal” alignment
A typical scoring system looks like2
- gaps = -2
- mismatches = -1
- matches = +1
but for example in my algorithms class, we used a dissimilarity scoring - gaps = +2
- mismatches= 0
- matches = +1
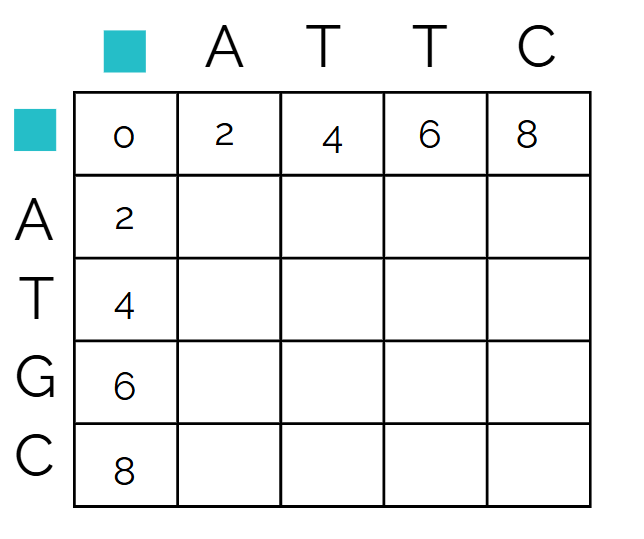
For this example, we’ll use ATTC and ATGC as the sequences
Filling out the matrix
Each cell can be represented as , where C is the individual cell, i is the row and j is the column. We move from cell to cell in particular directions based on matching/mismatching.
Here’s what the initial matrix looks like with the gaps initialized
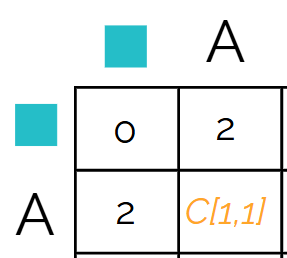
Let’s start with the first cell,
The path you choose defines the operation. So if you go diagonal, you choose to align the letters. If you go down/up, you insert a gap into s1 (horizontal). If you go left/right, you insert a gap in s2 (vertical).
Using the first cell, here are the options
- we can choose to align A vs A, meaning we need to choose diagonal. We need to add +1 to the number diagonal from - so that gives us 1
- we can choose to align s1 A (horizontal) to a gap in s2 (veritcal), meaning we’d move right. We need to add +2 to the number to the left of - so that gives us 4
- we can choose to align s2 A (veritcal) to a gap in s1 (horizontal), meaning we’d move down. We need to add +2 to the number to the top of - so that gives us 4
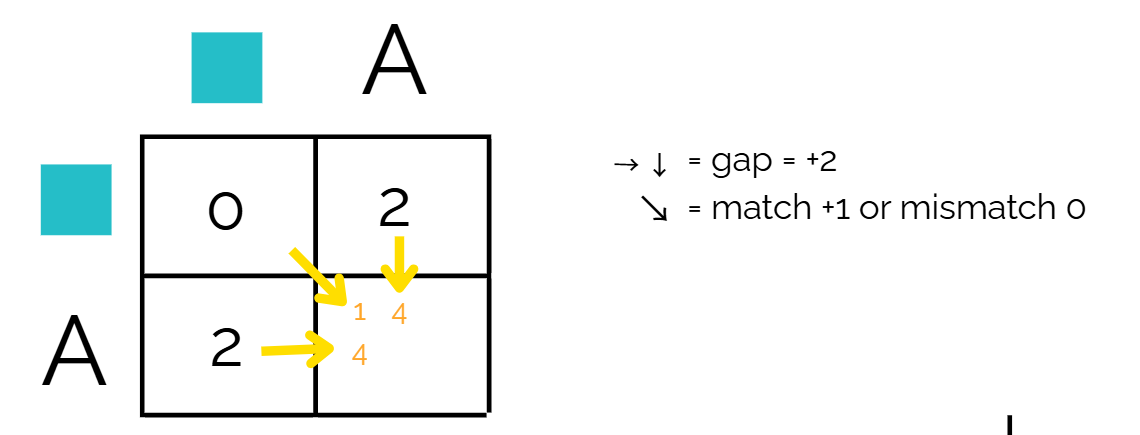
Since we’re using a disimilarity matrix for scoring, we want the lowest number. Out of the three options, 1 is the lowest number. Therefore we will use a diagonal path and match
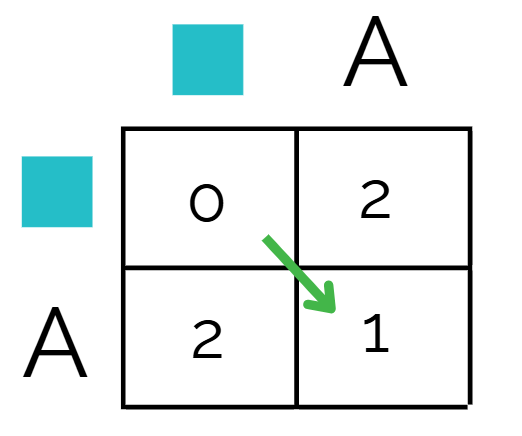
Continue for the rest of the matrix, going row by row. When you’re choosing the minimum number, keep in the mind the direction you chose to get that number - this will come in handy later.
The filled out matrix example is below
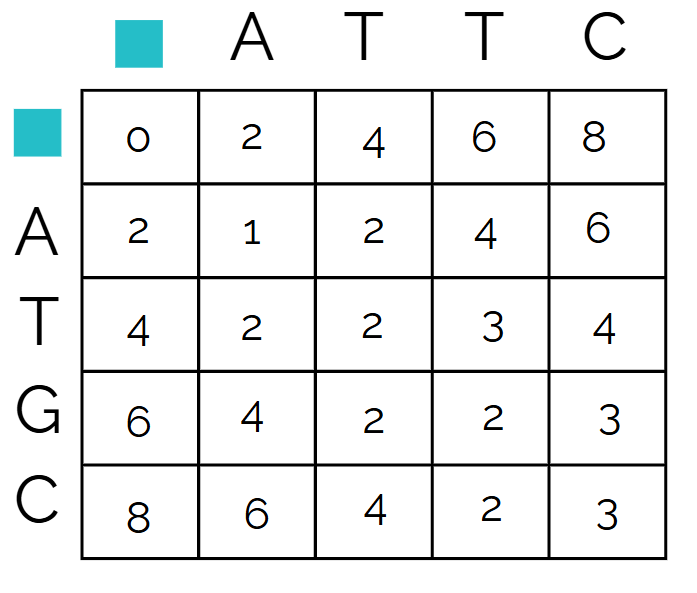
and the recorded paths taken to get each number - if there are more than one arrow leading to a cell, it means that multiple directions gave the same lowest number, meaning those two are possibilities
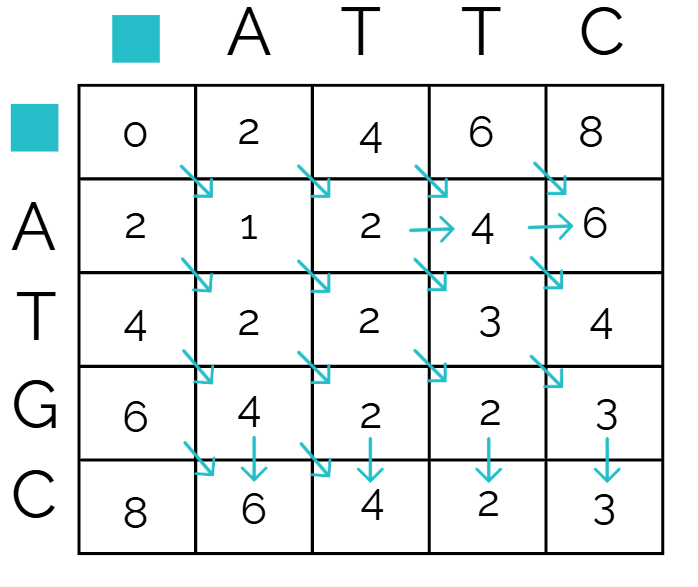
Pathfinding (traceback)
Traceback is how you find the best alignment using the score matrix, and you do this by starting from the bottom right corner, then looking at all the adjacent values.
Start from
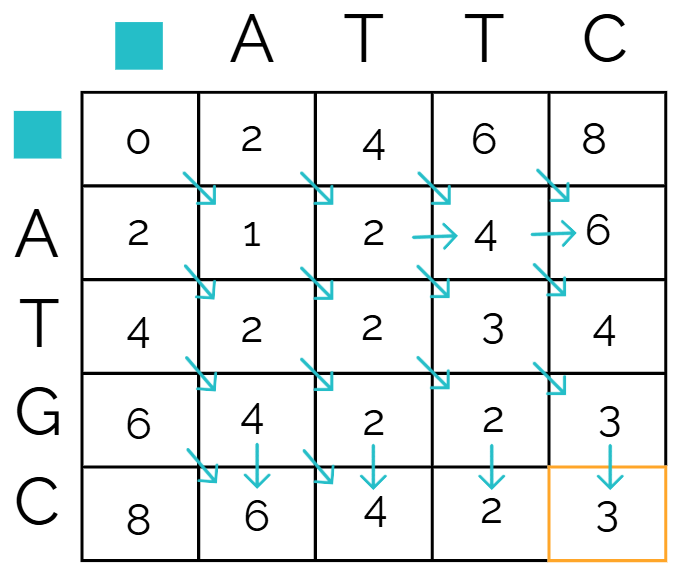
Then we look at the boxes above, diagonal, and to the left of
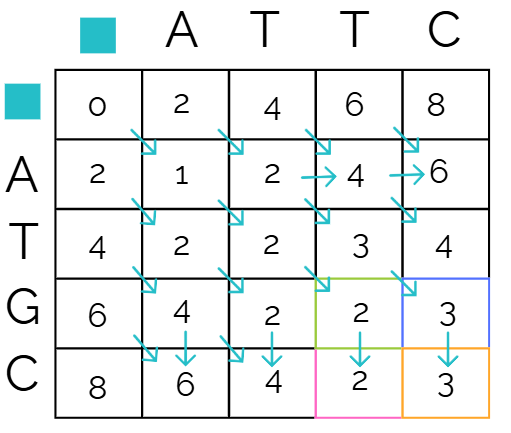
Remember our scoring system from earlier:
- diagonal = match or mismatch
- match = +1
- mismatch = 0
- up/down = gap = +2
- left/right = gap = +2
We will check the math on all the adjacent boxes to see which equations hold true. The valid equations determines the path we take. We will check if the diagonal, up, or left path equations are true.
Finding correct path via math validation
Note: this method might be overkill, but it’s the easiest one to breakdown for understanding what’s going on A quicker method that involves just looking at the min (dissimilarity) or max
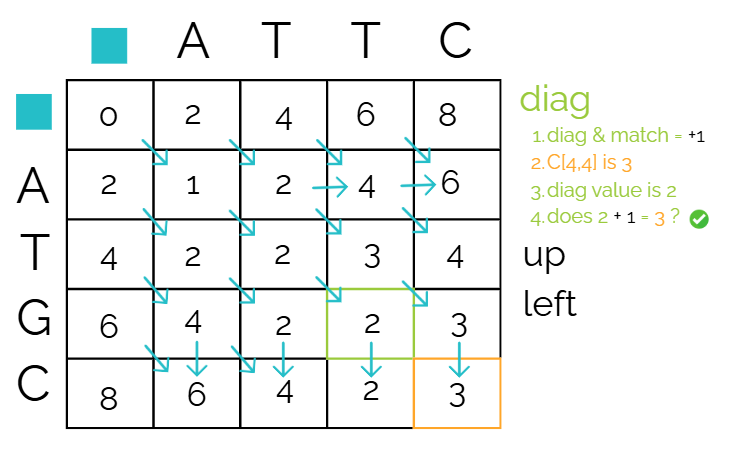
Check “diagonal”
Remember the reference cell is the bottom right.
We’re comparing our reference cell, to the diagonal cell first. Since it’s diagonal and a match (C vs C on the matrix), we need to check if 2 + 1 gives us our reference cell score. It does!
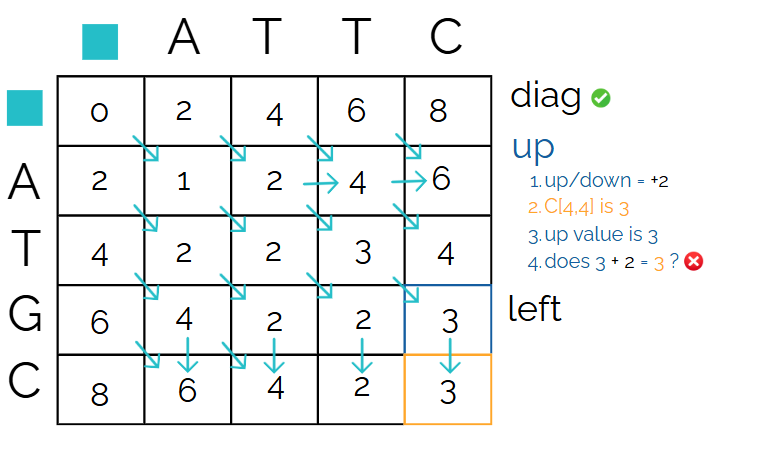
Check “up”
Now let’s compare the same reference cell to the cell above it. Since it’s up/down, it’s a gap. We need to check if 3 + 2 gives us our reference cell score. It does not.
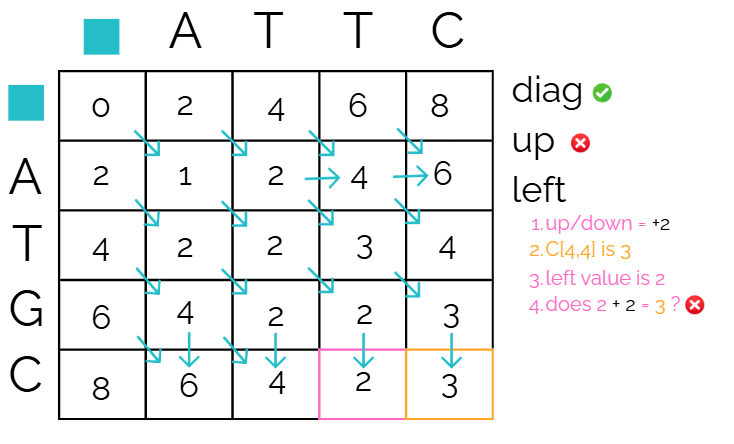
Check “left”
Finally compare the reference cell to the cell on the left. Since it’s left/right, it’s a gap. We need to check if 2 + 2 gives us our reference cell score. It does not.
Declare path
Out of the three options, only the diagonal one worked, so we mark that as the official path!
Continue this until you hit the top left corner, using the cell as the new reference cell
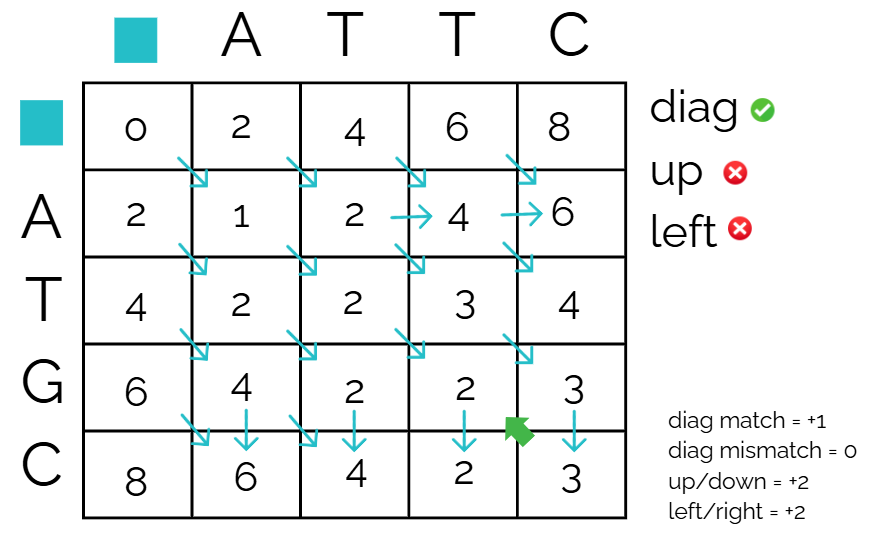
This is the declared path
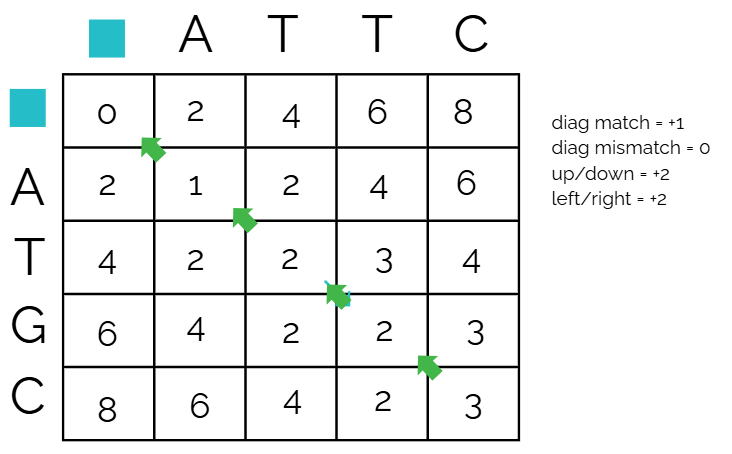
Align the sequences using traceback
The result of the traceback are as follows
S1: C T T A
S2: C G T A
so now we just need to flip it
A T T C
A T G C
this example doesn’t have any gaps - we got lucky with this problem. If there was, then we’d need to insert a gap into one of the sequences
dissimilarity or similarity matrix