Related: BNF 103-PAR Bioinformatics Algorithims
“How code slows as data grows”
- describes performance of an algo as the amount of data increases
- machine independent
- ignore smaller operations 0(n + 1) → 0(n)
Time complexity measures performance in terms of space and time: space is how much storage is needed, and time is how much time/iterations it takes. In general we always aim for a better time score than space score, because “we can always buy more space, but never buy more time”
Measured in number of steps it takes to complete the code. It explains why my BNF102 class spent so much time on counters
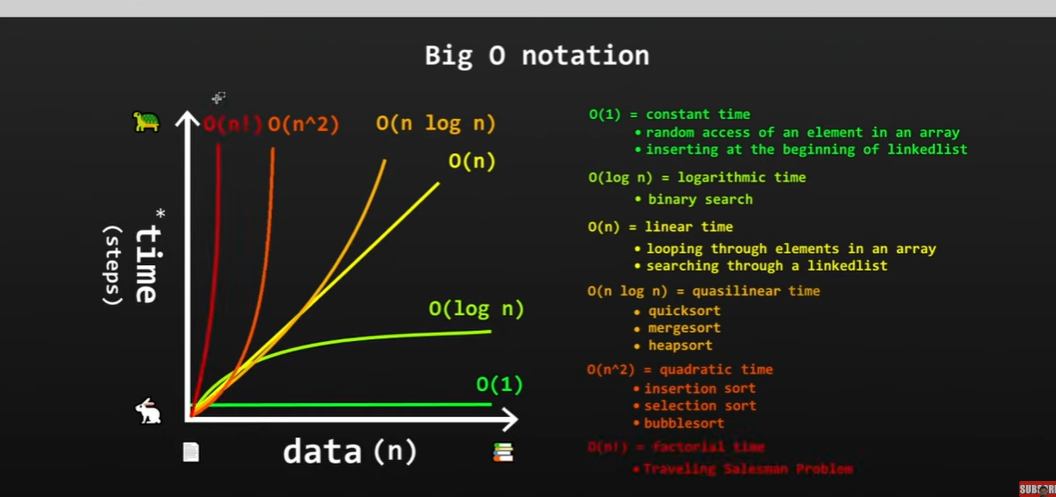
all time complexities
0(1) - constant time: same amount of time irrelevant of steps
- random access of element in an array
- inserting at beginning of a linked list
0(log n) - logarithmic time: takes increasingly less time to complete
- binary search
0(n) - linear time: as amount of data increases, amount of steps increases
- looping through elements in an array
- searching through a linked list
0(n log n) - quasilinear time: similar to linear time until we start to get to larger datasets
- quick sort
- mergesort
- heapsort
0(n^2) - quadratic time: extremely slow of large datasets, but can be faster with smaller datasets
- insertion sort
- selection sort
- bubblesort
0(n!) - factorial time
- traveling Salesman problem